Welcome! Bienvenidos! английский Willkommen! Benvenuti! الإنجليزية Welkom! ਅੰਗਰੇਜ਼ੀ Boas-Vindas! Hoşgeldiniz! Wellkom! 英语
- Join
- Professional
  - Engineering
  - FPGA
  - Resume
- Contact
- Sports
  - Triathlon
  - Training Log
- Gallery
- Calendar
- Türkçe
- İletişim
- Misc.
- Site Map

Online Black Scholes Calculator

The Black Scholes equation is a partial differential equation, which describes the price of the derivative (option or warrant) over time. In the financial world, a derivative is a financial instrument, whose value depends on the value of other, more basic, underlying variables. Very often the variables underlying derivatives are the prices of traded assets. A stock option, for example, is a derivative whose value is dependent on the price of a stock.

The extended Black Scholes models are jump-diffusion models, stochastic volatility models, local volatility models, regime-switching models, garch models. The Greeks are the sensitivities of the option prices to the various parameters.

If you need expertise on implementing Financial Algorithms or High Frequency Trading Algorithms on Hardware(RTL) in most efficient way, please contact me. The Black Scholes RTL IP Core can be downloaded here. I used this tool to verify the Hardware implementation of the financial functions. I hope it helps you too. Enjoy!

This tool is not qualified for financial uses and is not financially secure. You should not rely on it in financially-sensitive situations.

Model
Exercise
Method
Contract Type
Security Price Security Price Security Price (S) Use P0 [- P1] [- S] format for a range of stock price where S0: Starting value, P1: End Value of Range, S: Number of Steps. E.g. 5 will calculate for 5 value only. E.g. 5-20 will use default step number of 10 and will calculate for 5,5,5,6,...,10 values. E.g. 5-20-100 will calculate for 100 points between 5 and 20 values. Max step allowed is 100. If multiple fields are entered in range format, the first field will be used as the range. Others fields will be constant at the first value.
Strike Price Strike Price of Option Strike Price of Option (X) Use P0 - P1 format for a range of strike price. Use P0 - P1 - S format for a range of strike price with number of steps. E.g. 5-20 will use default step number of 10 and will calculate for 5,5,5,6,...,10 values. E.g. 5-20 - 100 will use 100 steps and will calculate for 5, 5.05, 5.1, 5.15....,10 values. Max step allowed is 100.
Expiration Date Expiration Date Expiration Date Expiration Date and Time to expiration are the same. Enter whichever is convenient and the tool will fill the other using todays date.
Time to expiration Time to expiration Time to expiration in years (T) If the time is in days, divide the value by 365 to convert to years.
Interest rate Risk-free Interest Rate Annual continuously compounded risk-free interest rate as % (r). For currency options the interest rate = foreign interest rate - local interest rate.
Dividend Yield Dividend Yield The stock's annual continuously compounded dividend yield as % (q)
Volatility Annualized Volatility σ = Annual stock price volatility as % (σ). Historical volatility is calculated as the standard deviation of logarithmic returns. Its value range is the same as the possible value range of standard deviation (from zero to positive infinite).	Implied
Implied Volatility Parameters
Option Price Number of Stocks This is needed for implied volatility calculation. This field is used when Implied is checked.
Warrant Parameters
# Stocks Number of Stocks This is needed for warrant price calculation. For regular option calculation this field is ignored.
# Warrants Number opf Warrants For normal option calculation set this field to 0. Any other value implies this is a warrant calculation. Warrant equations differ by a factor of n/(n+nw) So to value a warrant, multiply the value of an otherwise-identical call by n/(n+nw) where n is number of shares before the warrants are issued and nw is number of warrants
Trinomial Parameters
Barrier Type
Barrier Barrier For Trinomial only
Knockout Rebate Knockout Rebate For Trinomial only
Verbose Verbose Prints the interim components of the calculation.
This tool is AS IS. Use it on your own risk This is not a professional tool.	Example The stock of OptCal Co. currently sells for $370 per share. The annual stock price volatility is 0.1, and the annual continuously compounded risk-free interest rate is 0.04. The stock's annual continuously compounded dividend yield is 0.01. Based on the Black-Scholes formula what are the price of a call and a put option on OptCal Co. stock with strike price $485 and time to expiration of 2 years.

Price

First-Order Greeks

Delta (Δ)

Delta (Δ)

The delta of an option or a portfolio of options is the sensitivity of the
option or portfolio to the change in the price of the underlying security.
It is the rate of change of value with respect to the asset

The delta of a portfolio of options is just the sum of the deltas of all the individual positions.

Delta hedging means holding one of the option and short a quantity ∆ of the underlying.
Delta can be expressed as a function of S and t. This function varies as S and t vary.
This means that the number of assets held must be continuously changed to maintain a delta
neutral position, this procedure is called dynamic hedging.
Changing the number of assets held requires the continual purchase and/or sale of the stock.
This is called rehedging or rebalancing the portfolio.

Vega (ν)

Vega measures the calculated option value's sensitivity to small changes in volatility.
As with gamma hedging, one can vega hedge to reduce sensitivity to the volatility.
This is a major step towards eliminating some model risk, since it reduces dependence
on a quantity that is not known very accurately.

Theta (Θ)

Theta measures the calcualted option value's sensitivity to changes in time till maturity.
The Theta is related to the option value, the delta and the gamma by the Black-Scholes equation.
In a delta-hedged portfolio the theta contributes to ensuring that the portfolio earns the risk-free rate.

Rho (ρ)

Rho, ρ is the sensitivity of the option value to the interest rate used in Black-Scholes

Lambda (λ)

Lambda (λ)

Lambda (elasticity) is the percentage change in option value per percentage change
in the underlying security price, a measure of leverage, sometimes called gearing.

Second-Order Greeks

Gamma (Γ)

Gamma is the sensitivity of the delta to the underlying it is a measure of by
how much or how often a position must be rehedged in order to maintain a delta-neutral position.

Since gamma is a measure of sensitivity of the hedge ratio ∆ to the movement in
the underlying, the hedging requirement can be decreased by a gamma-neutral strategy.
This means buying or selling more options, not just the underlying.

Because the gamma of the underlying (its second derivative) is zero,
gamma cannot be added to position just with the underlying.
We can have as many options in our position as we want,
we choose the quantities of each such that both delta and gamma are zero.

Vanna

Vomma

Charm

Veta

Vera

Third-Order Greeks

Color

Speed

Ultima

Zomma

Dual Delta

Dual Gamma

Financial Raw Data

Assumptions of the Black and Scholes Model:

European exercise terms are used
Markets are efficient
No commissions, transaction costs or taxes are charged
Interest rates remain constant and known
Continuously compounded returns are lognormally distributed and independent over time
The volatility of continuously compounded returns is known and constant.
Future dividends are known, either as a dollar amount or as a fixed dividend yield.
The risk-free interest rate is known and constant.
It is possible short-sell costless and to borrow at the risk-free rate.

φ	The standard normal probability density function.
Φ	The standard normal cumulative distribution function.
S	Security Price
X	Strike Price
r	Risk-Free Rate
q	Annual Dividend Yield
τ	Time to Maturity τ = T-t
σ	Volatility
d1
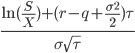
d2
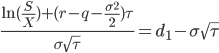
		Calls	Puts
Option Value (V)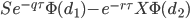
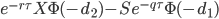Delta
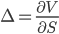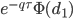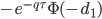Vega
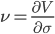
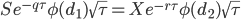Theta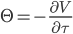
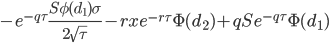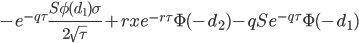Rho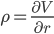
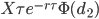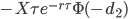Lambda	Delta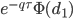* (S/V)	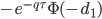* (S/V)	* (S/V)
Gamma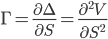
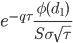Vanna
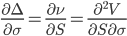
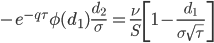Charm
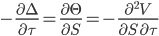
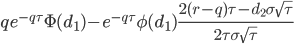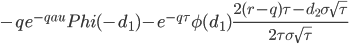Speed
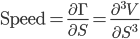
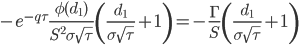Zomma
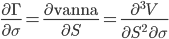
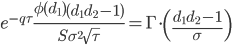color
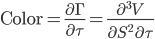
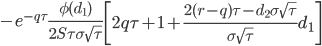Veta
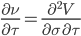
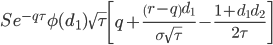Vomma
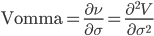
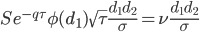
Ultima
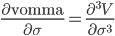
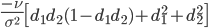Totto	dVomma/dT
Dual Delta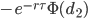
Dual Gamma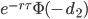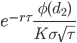

Options

An option is a derivative that specifies a contract between two parties for a future transaction, known as an exercise, on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the corresponding obligation to fulfill the transaction. There are two types of option. A call option gives the holder the right to buy the underlying asset by a certain date for a certain price. A put option gives the holder the right to sell the underlying asset by a certain date for a certain price. The price in the contract is known as the strike price. The date in the contract is known as the expiration date.

The difference between an American and European option is that the American option can be exercised at any time up to the expiration date, whereas the European option can be liquidated only on the settlement date. European options can be exercised only on the expiration date. The American option is "continuous time" instrument, while the European option is a "point in time" instrument. Options are just tools to evaluate underlying assets contingent to a specific event, or viceversa to understand the probabilities implied in the price that an event will happen. The strength of the results is directly correlated to the quality of the inputs used in the model.

All the material listed and linked at this World Wide Web domain are strictly private property and copyrighted. © Copyright -∞-∞ Levent Ozturk. All rights reserved. Reproduction or use of any material, documents and related graphics and any other material from this World Wide Web server is strictly prohibited. Site Map

Call Price	Put Price
Call Delta	Put Delta
	Vega
Call Theta	Put Theta
Call Rho	Put Rho
	Lambda
	Gamma
	Vanna
	Vomma
Call Charm	Call Charm
	Veta
	Vera
	Coloro
	Speedo
	Ultima
	Zomma
Call Double Delta	Put Double Delta
	Double Gamma