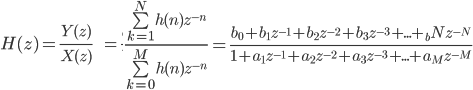, frequency response and impulse response based on the entered filter specifications.
FIR filters have inherent stability when implemented in non-recursive form, linear phase, simple extensibility to multirate cases. FIRs are convolutional, No phase distortion and Direct Form Structure.
Filter types are:
Enter the filter specification and the tool will calculate the FIR filter coefficients and plot the frequency response.
Max number of coefficients is limited to 128 to prevent CPU overloading.
A quick guide for DSP design is provided to help understand the FIR filter design. If you need help on Filter Design, choosing filter Specifications, creating a special filter structure, or any Digital Signal Processing questions in general,
.
The tool is written in Perl. I use this tool to design FIR filters. I hope it helps to you too. Enjoy...
Digital Filter
Signal types are
- Analog: continuous time, continuous level
- Quantized: continous time, discrete level
- Sampled: discrete time, continuous level
- Digital: discrete time, discrete level
"Digital" filter are "sampled" (= time discrete) signals, not necessarily on digital (quantized) ones. So
"Discrete Time Filter" is more accurate but less popular and familiar.
Digital filters are
time invariant which means their output does not depend explicitly on time.
Digital filters are
linear which means output of the filter is a linear function of its input.
Filters are completely defined by their
transfer function.
Becasue Digital Filters are linear and time invariant (LTI), their transfer function can be completely characterised by their
time response(
impulse responseImpulse Response
The impulse that is referred to in the term impulse response is generally a short-duration time-domain signal.
For continuous-time systems, this is the Dirac delta function δ(t),
while for discrete-time systems, the Kronecker delta function δ[n] is typically used.
The output of the filter is simply the input signal convolved with the impulse response function. The center term of the convolution is the output.
, step response or ramp response), or
frequency response.
Frequency response = FFT(impulse response)
Impulse Response = Inv Laplace(Transfer function)
Digital filters are
convolutional because the output of the filter is simply the input signal convolved with the impulse response function.
Based on the transfer function (or impulse response), Digital Filters are categorised as
finite (FIR) or
infinite (IIR) filters.
Finite impulse response (FIR) filters are
non-recursive since they don't have a feedback form output to input (non-recursive transfer function). Output eventually becomes 0 when input becomes 0.
Infinite impulse response (IIR) filters are
recursive since they have a feedback form output to input (recursive transfer function). Output may never dies down even if the input goes to 0 in certain conditions.
The filter output depends only on past and present inputs is
casual. A filter whose output also depends on future inputs is non-causal, whereas a filter whose output depends only on future inputs is anti-causal. Only casual filters are
realizable.
Transfer function for a casual LTI digital filter has the form:
in the Z-domain
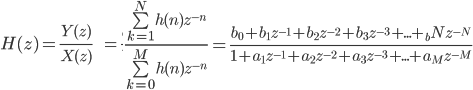
In time domain;

Notice the convolution and recursiveness.
If the denominator is made equal to unity (1) i.e. no feedback, then this becomes a FIR.
If the denominator is not 1 i.e. feedback, then this becomes an IIR.
Roots of the numerator polynomial are
zeros. When input is equal to one of the roots of the numerator polynomial, the output becomes 0.
Roots of the denominator polynomial are
poles. When input is equal to one of the roots of the denominator polynomial, the output becomes infinite(looks like a pole on plot).
The
filter order equals the number of poles or zeros, whichever is greater.
z Domain: the Fourier transform expresses a function or signal as a series of modes of vibration (frequencies),
s Domain: the Laplace transform resolves a function into its moments. (s is complex).
A digital filter structure is said to be
canonic if the number of delays in the block diagram representation is equal to the order of the transfer function.
Filter impulse response types are defined as follows:
Type 1 — Even-order symmetric coefficients
Type 2 — Odd-order symmetric coefficients
Type 3 — Even-order antisymmetric coefficients
Type 4 — Odd-order antisymmetric coefficients
For the highpass and bandstop configurations filter order should be even as for odd orders, the frequency response at the Nyquist frequency is 0.
Order and symmetry is determined by the chosen design method described below.
Filter Design
Filter design is as easy as
1. Filter Description: describe freq response
2. Design Method: find coefficients
3. Implement: select implementation
1. Filter Specification
First step in designing a Linear time Invariant Time discrete convolutional finite/infinte recursive/non-recursive casual filter is to determine its sepecifications.
Filter frequency response is most commonly used to specify a filter. Filter frequency response types may be categorized as Lowpass, Highpass, Bandpass, Bandstop, Arbitrary. Frequency response tells the output magnitude for each frequency or gain for unit input for each frequency. The accuracy of the frequency response is determined by the specification method defiend below.
Frequency response can be specified as:
- cutoff frequency
- Passband frequency, passband amplitude, stopband frequency, stopband amplitude
- Transition frequency, transition width, pass band ripple, stop band ripple
- a list of magnititudes, phase) with their corresponding frequencies (frequency to mag,phase pair table)
2. Desing Methods
Once the filter specification is defined, design method is choosen. Design method is the method to find the impulse response based on the filter specifications.
2.1. Window Method (Aproximation)
Matlab fir1 function uses window method.
This method starts with ideal frequency response which is rectangular which is 1 for all the pass band frequencies, and equal to 0 for all the stop band frequencies.
IFFT this freq response to get the impulse response. FFT of ideal (rectangular) frequency response is sinc function in time domain.
Sinc impulse response is infinite. Apply window function to make the response finite.
The simplest window is rectangular window which simpy truncates the impulse response. Most common window functions are
- BARTLET
- HANNING
- HAMMING
- BLACKMAN
As a result of windowing side lobes will appear in the frequency response of final filter.
The window method is basically used for the design of prototype filters like the low-pass, high-pass, band-pass etc. They are not very suitable for designing of filters with any given frequency response.
2.2. Frequency Sampling method
Matlab fir2 function uses frequency sampling method.
firrcos is also fr sampling . Instead of measuring fr response, define the transition band values as rcosine.
This method also takes IFFT of the desired freq response. In this method, the frequencty samples are the same as number of requred filter coefficients. So after IFFT no windowing is required.
If you started with the filter length in the frequency domain, there would be no further truncation in the time domain and that specifically is the frequency sampling method. The result is precise response at the frequency sampling locations.
The frequency sampling technique is suitable for designing of filters with a given magnitude response.
The ideal frequency response of the filter is approximated by placing appropriate frequency samples in the z- plane and then calculating the filter co-efficients using the IFFT algorithm.
The disadvantage of the frequency sampling technique was that the frequency response gave errors at the points where it was not sampled.
In order to reduce these erros the different optimization technique for FIR filter design were presented wherein the remaining frequency samples are chosen to satisfy an optimization criterion.
2.3. Least Squares Method / Weighted Least Squares Method (Optimisation)
(firls)(Aproximation)(Optimisation method or optimal filter design method)
2.4. Parks-McClellan method (aka Equiripple Method, Optimal, or Minimax method) (Optimisation)
firpm, firgr (Aproximation)(Optimisation method or optimal filter design method)
The Remez exchange algorithm is commonly used to find an optimal equiripple set of coefficients.
Equiripple FIR filters can be designed using the FFT algorithms as well. Inverse FFT the freq response.
3. Filter Realization / Implementation
Then filter realization type is choosen
- Direct Form I (delay multiply add)
- Direct Form II (delay multiply add)
- Cascaded second-order sections
- Direct Form I and II transpose (multiply delay add)
- Series/cascade lower (typical second) order subsections
- Parallel lower (typical second) order subsections
- Continued fraction expansion
- Lattice and ladder
- One, two and three-multiply lattice forms
- Three and four-multiply normalized ladder forms
- ARMA structures
- State-space structures:
- optimal (in the minimum noise sense): (N+1)^2 parameters
- block-optimal and section-optimal: 4N-1 parameters
- input balanced with Givens rotation: 4N-1 parameters
- Coupled forms: Gold Rader (normal), State Variable (Chamberlin), Kingsbury, Modified State Variable, Zölzer, Modified Zölzer
- Wave Digital Filters (WDF)
- Agarwal–Burrus (1AB and 2AB)
- Harris–Brooking
- ND-TDL
- Multifeedback
- Analog-inspired forms such as Sallen-key and state variable filters
- Systolic arrays
Pulse shaping
Square wave (10101 pattern) has two freq component 0Hz (at 1 or 0 state), infinite Hz at transition. Pulse shaping softens! the transition so the frequency components (highest chage rate of the signal in time) of the signal remain within the bandwidth.
http://en.wikipedia.org/wiki/File:Raised-cosine-filter.png
softening or shaping is mesauerd by the roll-off factor.
Some of the pulse shaping filters are The trivial boxcar filter, Sinc shaped filter, Raised-cosine filter, Gaussian filter.
Matched Filter
The distinguishing characteristic of a Matched Filter is the step response approximates a ramp, and the impulse response approximates a pulse.
The purpose of the Matched Filter is to maximize the signal to noise ratio and to minimize the probability of undetected errors received from a signal.
Using a Matched Filter at the Receiver
Sometimes the filtering is split between the transmitter and receiver. The data stream is upsampled and filtered at the transmitter and then the transmitted signal is filtered and downsampled by a matched filter at the receiver. This approach is very popular because, for a given processing power, using two square root raised cosine filters (one in the transmitter and one in the receiver) provides better stopband attenuation than using a raised cosine filter in the transmitter and a downsampler in the receiver.
using a matched filter instead of a downsampler at the receiver improves the BER substantially for relatively low SNRs.
Notes: