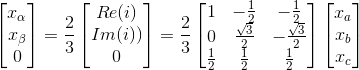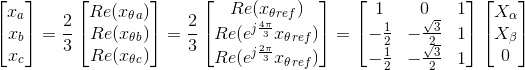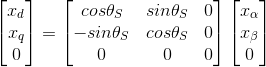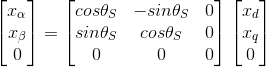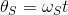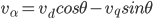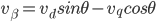Online Field-Oriented Control (Clarke-Park) Calculator
This online program calculates Clarke and Park transforms for a given vector. The Inverse Park Transform function calculates the Inverse Park Transform portion of the field-oriented control (FOC) commutation algorithm, which modifies the flux,torque (d,q) rotating reference frame in a two phase orthogonal system (alpha,beta)..
Enter the vector values and the tool will calculate and plot the transformed output.
I use this tool to verify FOC vectors in the field. I hope it helps to you too. Enjoy...
Notes:
- All the values will be calculated both forward and backward from the last changed value
Machine Transformations
Space Vector
A Space Vector is represented by a complex number having
- a magnitude equal to the peak amplitude of the variable and
- an angle equal to the angular position of this positive peak value.
Clarke Transform (Notation)
Clarke is simply (only for 3-phase system where phases are equally apart) taking a reference angle (Stator Reference Frame)
(or phase) which is Θa for Clarke and typing the i space vector in real (α) and imaginary (β) components.
number of Phase = 3
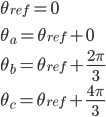 =>
=>
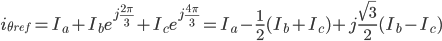
Scale by 2/3 for convenience.
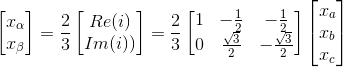 =>
The clarke Transformation matrix T is
=>
The clarke Transformation matrix T is
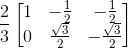
In order for the transformation to be invertible, 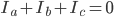 equation as a third variable,
known as the zero-sequence component for a balanced system, is added.
equation as a third variable,
known as the zero-sequence component for a balanced system, is added.
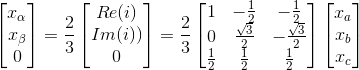
For reverse transform T matix is simply inverted which means projecting the vector i onto respective a,b, and c axes.
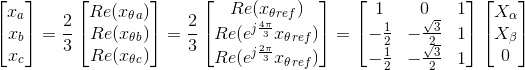
Other correct but confusing and incomplete definitions are:
The Clarke or (α β), transform is a space vector transformation of time-domain signals (e.g. voltage, current, flux, etc) from a natural three-phase coordinate system (ABC) into a stationary two-phase reference frame (α β 0).
CLARKE converts balanced three phase quantities into balanced two phase orthogonal quantities;
For n phase system the (n=3), and phases are equally apart from each other (120), take one phase as reference angle (a)
i = ia+ib+ic+...+in
ia+ib+ic+...in=0
The above relation concentrates the effects of three phase current into a single complex variable.
Clarke_Transform
Three-phase voltages varying in time along the axes a, b, and c, can be algebraically transformed into two-phase voltages, varying in time along the axes α and β by the following transformation matrix:
The inverse transformation can also be obtained to transform the quantities back from two-phase to three-phase:
Park Transform (Notation)
Park transform is describe in rotator Reference frame.
Park’s Transform is usually split into CLARKE transform and one
rotation;
It is moving at θs and its PARK coordinates are constant in (d,q) rotating frame.
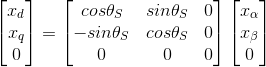
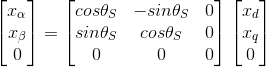
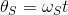
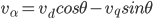
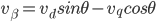
The Inverse Park Transform function calculates the Inverse Park Transform portion of the field-oriented control (FOC) commutation algorithm, which modifies the flux,torque (d,q) rotating reference frame in a two phase orthogonal system (alpha,beta).
va,vb = IPT(vd,vq,teta)
Single axis, Four Axis
Where valpha is the alpha voltage. Specifies the alpha voltage calculated by the Inverse Park Transform for the Space Vector Modulation function.
vd is the direct voltage. Specifies the direct voltage value calculated by the flux/torque loop for use with the Inverse Park Transform.
vq is the quad voltage. Specifies the quad voltage value calculated by the flux/torque loop for use with the Inverse Park Transform.
vbeta is the beta voltage. Specifies the beta voltage calculated by the Inverse Park Transform for the Space Vector Modulation function.
θ is the angle of rotation for the transformed reference frame. Specifies the calculated flux angle for the Park and Inverse Park transforms, in pi radians.
PID: proportional-integral-derivative feedback.
PID
Proportional: Current, Integral: Past, Derivative:Future
Hall A,B,C->Hall Angle Calculator->Flux Angle Calculator--->Same ParkT
U,V Current -> ClarkT->ParkT->PI Motor Fulux and Torque Control(Cascaded PI Loop, PID Motor Control)->IPT->SVM->PEM ->U,V,W
Space Vector Modulation
All the material listed and linked at this World Wide Web domain are strictly private property and copyrighted.
©
Copyright -∞
-∞
Levent Ozturk. All rights reserved. Reproduction or use of any material, documents and related graphics and any other material
from this World Wide Web server is strictly prohibited.
Site Map


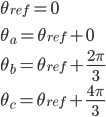 =>
=>
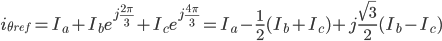
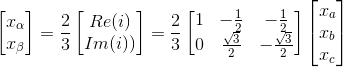 =>
The clarke Transformation matrix T is
=>
The clarke Transformation matrix T is
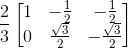
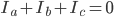 equation as a third variable,
known as the zero-sequence component for a balanced system, is added.
equation as a third variable,
known as the zero-sequence component for a balanced system, is added.