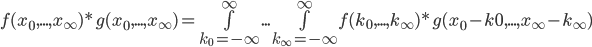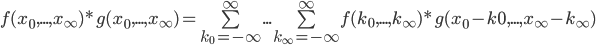Online Multidimensional Convolution Calculator
This free online program calculates the Convolution matrice of two input matrices.
The Convolution Function is represented as C = A * B where A,B are inputs and the C is the convolution output.
This tool supports up to 4 dimension input matrices (A and B).
Each dimension can have up to 8 terms.
Results will include the calculated values of the convoluded matrice.
The input terms used to calculate each term of the convoluded matrice is also provided.Just point to the result term to see the input convolution terms used to calculate the result term.
The calculation matrices are of limited size, but the actual convolution is over infinite size. This means there will be terms out of matrice bounds in the result equation which are simply 0 (inefective).
The online convolution calculator is used for
math calculations,
polynomial calculations,
image processing or
digital signal processing calculations. You may visit my
Engineering page for other engineering tools. The online convolution tool helps me for error free calculations. I hope it helps to you too. Enjoy...
Notes:
- Out of bound terms both in negative and positive direction are highlited red and the value of these terms are 0.
- This tool supports up to 4 dimension and 8 terms per dimension and term values can be between 0-256. If you need to calculate higher dimension and higher order convolution, contact me and I can enable the higher dimension and term calculation.
- If you just need high order polynomial (1 dimension) convolution, you may use the CRC tool. CRC tool allows up to 200 term polynomial (1 dimension) convolution.